两道与抛物线有关的(解析)几何题目
两个抛物线的性质都可以在cut the knot中找到。
题目一
在初三下学期第一次一试练习中,第11题是一道解析几何题:
求证若一条抛物线旁切于一个三角形,则三角形的外接圆过抛物线的焦点。
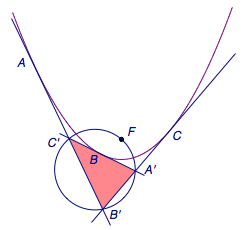
本题的特例在2022年全国中学生数学奥林匹克竞赛新疆赛区选拔赛中也出现过。事实上,这个结论被称做“兰伯特定理”(Lambert’s theorem)。能找到的最早来源是书籍《几何观下的圆锥曲线》(Conic sections, treated geometrically),其于1890年出版。一个证明可在Solution of Sondow’s problem: a synthetic proof of the tangency property of the parbelos中找到,先证明抛物线焦点到抛物线上任一点切线的垂足在过抛物线顶点的切线上的引理,然后由西姆松线定理可证结论。
题目二
在初三下学期最后一次一试练习中,第11题还是一道解析几何题:
> 已知抛物线 $C:y^2=2px(p\gt 0)$ 的焦点为 $F$, 记 $\angle MNx$ 为向量 $\overrightarrow{NM}$ 与 $x$ 轴正方向所成角的大小. 若对 $C$ 上不同象限的两点 $P$、$Q$ (点 $P$ 在 $Q$ 上方), 有一个点 $R$ 满足$$2\angle PRx=\angle PFx, 2\angle QRx=\angle QFx,$$
证明: $\triangle PFR \sim \triangle RFQ$.
由抛物线的光学性质,可以知道PR和QR均为抛物线的切线。这个结论并没有一个公认的名字,但它同样很早就被人所知,和兰伯特定理一样,在书籍《几何观下的圆锥曲线》中亦有出现。它也可以用来证明兰伯特定理。下图为另一本书中的证明,证明过程同样用到了上述引理。

一道平面几何题目的两种解法
题目
平面内有$\triangle ABC$,作其外接圆$\odot O$,作垂心$H$,设$\angle A$外角平分线与$\odot O$交于点$A$和$N$。延长$NH$与$\odot O$交于点$D$。设过$O$直线与$AB$交于$E$,与$AC$交于$F$,且$AE=AF$。延长$DE$与$\odot O$交于点$J$,延长$DF$与$\odot O$交于点$K$。求证:$J$和$K$分别为$C$和$B$的对径点。
解法一
令J’为C的对径点,M为N的对径点。作HM中点G,AB中点I。设AM与CD交于X。令圆G为以HM为直径的圆。
首先,通过导角可知,$\triangle OIE \sim \triangle J’MC$,所以$OE:J’C=IO:MJ’$。
同时由垂心性质,I是HJ’中点,所以2IG=J’M且IG∥JM,又因为J’C=2J’O,所以$OE:J’O=IO:IG$。
再进行导角,可知$\angle OIG=\angle J’OE$,所以$\triangle OIG \sim \triangle EOJ’$。所以$\angle IOG=\angle J’EO$。
由于圆O和圆G交于MD两点,所以OG⊥MD。通过导角可得$\angle CXM=\angle IOG$。从而$\angle CXM=\angle J’EO$。再因为AM⊥OE,所以CD⊥J’E。
因为CD垂直于J’D,所以J’DE共线。而JDE也共线,所以J与J’重合,J为C的对径点。同理,K为B的对径点。
解法二
作出△AEF垂心G。作BF中点S,CE中点T。令圆S以BF为直径,圆T以CE为直径,M为N的对径点。设$R$为圆O半径。
作H到AC边上垂足$H_1$,到AB边上垂足$H_2$。
则$BCH_1H_2$四点共圆。所以$BH\cdot HH_1=CH\cdot HH_2$。
又因为$H_1$在圆S上,$H_2$在圆T上。所以H关于圆S和圆T的圆幂相等。
同理,G关于圆S和圆T的圆幂相等。
所以,直线HG为圆S和圆T根轴。
由于
$$
\overrightarrow{NA}\cdot\overrightarrow{NC}-\overrightarrow{NA}\cdot\overrightarrow{NB}\
=\overrightarrow{NA}\cdot\overrightarrow{BC}\
=|NA|\times|BC|\times \cos{\langle\overrightarrow{NA},\overrightarrow{BC}\rangle}\
=2R\sin{\frac{B-C}{2}} \times 2R\sin{A} \times (-\cos{\frac{B-C}{2}})\
=-2R^2\sin{(B-C)}\sin{A}\
=2R^2\sin{(C-B)}\sin{A}\
=2R^2\times2\sin{\frac{C-B}{2}}\sin{A}\times\cos{\frac{C-B}{2}}\
=\frac{R\sin{(B+\frac{A}{2})}}{\cos{\frac{A}{2}}}\times2R\sin{\frac{B+C}{2}}\times(\cos(A+\frac{B-C}{2})-\cos(A+\frac{C-B}{2}))\
=|AE|\times|NB|\times (\cos{\langle\overrightarrow{AF},\overrightarrow{NB}\rangle}-\cos{\langle\overrightarrow{AE},\overrightarrow{NC}\rangle})\
=\overrightarrow{AF}\cdot\overrightarrow{NB}-\overrightarrow{AE}\cdot\overrightarrow{NC}\
$$
所以$\overrightarrow{NE}\cdot\overrightarrow{NC}=\overrightarrow{NB}\cdot\overrightarrow{NF}$。
所以$|NS|^2-|SB|^2=(\overrightarrow{NS}+\overrightarrow{SB})\cdot(\overrightarrow{NS}-\overrightarrow{SB})=\overrightarrow{NB}\cdot\overrightarrow{NF}=\overrightarrow{NC}\cdot\overrightarrow{NE}=(\overrightarrow{NT}+\overrightarrow{TC})\cdot(\overrightarrow{NT}-\overrightarrow{TC})=|NT|^2-|TC|^2$
于是N到圆S和圆T的圆幂相等。所以NGH共线。
因为AEMF是菱形,所以∠GEM=∠GFM=90°。而∠GDM=∠NDM=90°,所以得知GEMDF五点共圆。所以有$\triangle MEJ \sim \triangle MFK$。而因为ME=MF,所以MJ=MK。又因为M为弧BC中点,所以BK与CJ交点位于直线MN上。
根据帕斯卡定理,AB与DJ交点,AC与DK交点,BK与CJ交点三点共线。所以BK与CJ交点位于直线EF上。而EF与MN交于点O,且两条直线不重合。所以BK和CJ交点为O。因此J为C的对径点,K为B的对径点。