by @abcxyz & @liboyuan08
作为高二上学期的数学期末,这次考试的21题出了一道比较困难的解析几何题,让我们一起来看一下吧!
题目
已知椭圆 $ E: \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\ (a>b>0) $ 上、下顶点间的距离为 $4$,且离心率为 $\frac{\sqrt{6}}{3}$。
(I) 求椭圆 $E$ 的方程;
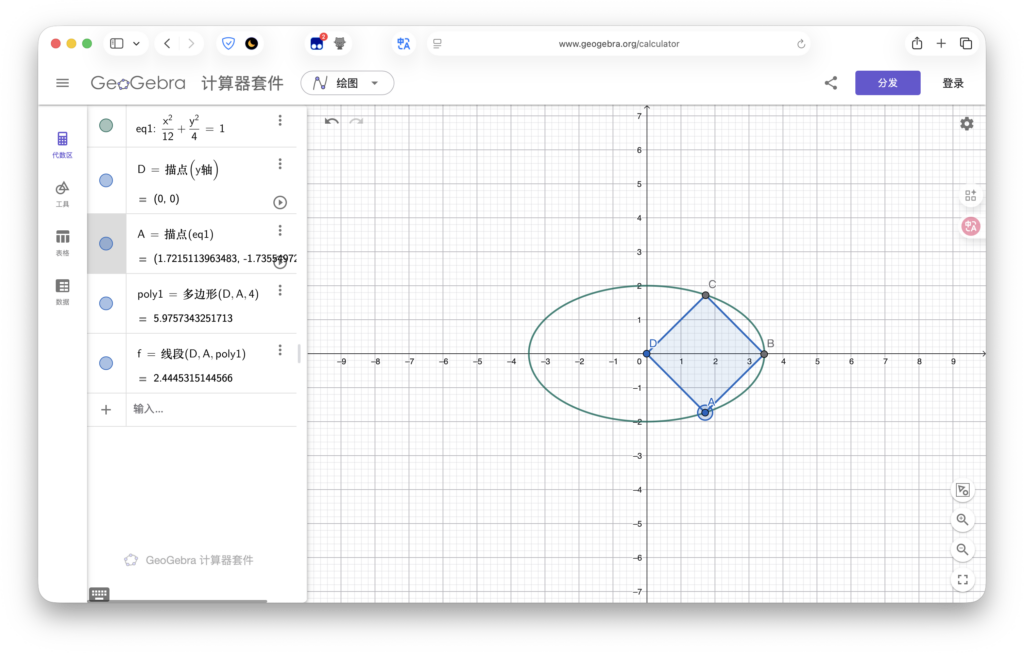
(II) 试问:是否存在正方形 $ABCD$,使得顶点 $A,B,C$ 在椭圆 $E$ 上,且顶点 $D$ 在 $y$ 轴上?若存在,求出所有正方形 $ABCD$ 的边长;若不存在,说明理由。
解答
导览:所有使用“引用”格式的部分即为卷面过程。
因为本文包含2种方法的完整卷面过程,所以文章会很长,大家挑自己需要的重点内容看即可。
第一问
第一问就是一个常规的求椭圆方程,注意短轴长是 $2b$ 即可。我们直接看区里给的答案:
由题意,得
$$
\begin{cases}
2b = 4, \
\frac{c}{a} = \frac{\sqrt{6}}{3}, \
c^2 = a^2 – b^2.
\end{cases}
$$
解得 $a^2 = 12$,$b^2 = 4$。所以椭圆 $E$ 的方程为
$$
\frac{x^2}{12} + \frac{y^2}{4} = 1.
$$
第二问
第二问涉及到正方形这个几何图形。我们不难发现,只要确定了正方形一条对角线两端的两个点,那么正方形的位置便唯一确定了。
于是我们考虑确定 $A,C$ 两个位于椭圆上的点。
方法1:直线与椭圆联立
我们考虑先设出直线 $AC$ 的方程,与椭圆方程联立,两个解即为 $A,C$ 两点。然后我们可以使用韦达定理解决问题。这也是参考答案中给出的思路。
这时一定不要忘记讨论 $k_{AC}$ 不存在的情况。这种情况价值2分。
当直线 $AC$ 斜率不存在时,
假设正方形 $ABCD$ 存在,由对称性知 $D(0,0)$,不妨设 $B(2\sqrt{3},0)$,$A(\sqrt{3}, s)$ ($s > 0$)。将 $A(\sqrt{3}, s)$ 代入椭圆 $E$ 的方程,得
$$
\frac{(\sqrt{3})^2}{12} + \frac{s^2}{4} = 1,
$$
解得 $s = \sqrt{3}$。此时 $A(\sqrt{3}, \sqrt{3})$,$C(-\sqrt{3}, \sqrt{3})$,四边形 $ABCD$ 恰为正方形,其边长为 $\sqrt{6}$。
下一步是解决 $k$ 存在的情况。这时又有两种不同的思路,其中一种是先找到 $A,C$ 的中点 $M$,再引一条过 $M$ 且垂直于 $AC$ 的直线与 $y$ 轴联立,得到 $D$ 的坐标,并验证 $|AC|=|BD|$。
我们先跟着参考答案来看看这种思路。因为涉及到 $k_{BD}$ 的存在性,所以需要讨论 $k_{AC}=0$ 的情况:
当直线 $AC$ 斜率为 0 时,
假设正方形 $ABCD$ 存在,由对称性不妨设 $B(0, -2)$,$A(t, t-2)$ ($t > 0$)。
将 $A(t, t-2)$ 代入椭圆 $E$ 的方程,
$$
\frac{t^2}{12} + \frac{(t-2)^2}{4} = 1,
$$
解得 $t = 3$。此时 $A(3,1)$,$C(-3,1)$,$D(0,4)$,正方形 $ABCD$ 的边长为 $3\sqrt{2}$。
然后剩下的一般情况直接设 $AC: y=kx+m$ 即可。
就算没有解出坐标,有了韦达定理过程后,还可以得到2分。
当直线 $AC$ 斜率存在且不为 0 时,设 $AC$ 的方程为 $y = kx + m$ ($k \neq 0$),
由
$$
\begin{cases}
y = kx + m, \
x^2 + 3y^2 = 12,
\end{cases}
$$
得
$$
(3k^2 + 1)x^2 + 6kmx + 3m^2 – 12 = 0.
$$
判别式 $\Delta = (6km)^2 – 4(3k^2 + 1)(3m^2 – 12) > 0$,整理得 $4k^2 + 12 – m^2 > 0$。设 $A(x_1, y_1)$,$C(x_2, y_2)$,则
$$
x_1 + x_2 = -\frac{6km}{3k^2 + 1}, \quad x_1x_2 = \frac{3m^2 – 12}{3k^2 + 1}.
$$设 $AC$ 中点为 $M$,
$$
x_M = -\frac{3km}{3k^2 + 1}, \quad y_M = kx_M + m = \frac{m}{3k^2 + 1},
$$
则
$$
M\left(-\frac{3km}{3k^2 + 1}, \frac{m}{3k^2 + 1}\right).
$$因此直线 $BD$ 的方程为
$$
y – \frac{m}{3k^2 + 1} = -\frac{1}{k}\left(x + \frac{3km}{3k^2 + 1}\right).
$$令 $x = 0$,则
$$
y_D = \frac{m}{3k^2 + 1} – \frac{1}{k} \cdot \frac{3km}{3k^2 + 1} = \frac{m – 3m}{3k^2 + 1} = \frac{-2m}{3k^2 + 1},
$$
所以 $D\left(0, \frac{-2m}{3k^2 + 1}\right)$。由于 $M$ 为 $BD$ 中点,则
$$
B\left(-\frac{6km}{3k^2 + 1}, \frac{4m}{3k^2 + 1}\right).
$$将 $B$ 点坐标代入椭圆 $E$ 的方程,整理得
$$
\frac{(-6km)^2}{12(3k^2 + 1)^2} + \frac{(4m)^2}{4(3k^2 + 1)^2} = 1,
$$
即
$$
\frac{36k^2m^2}{12(3k^2 + 1)^2} + \frac{16m^2}{4(3k^2 + 1)^2} = 1,
$$
化简得
$$
\frac{3k^2m^2}{(3k^2 + 1)^2} + \frac{4m^2}{(3k^2 + 1)^2} = 1,
$$
进一步整理得
$$
\frac{m^2(3k^2 + 4)}{(3k^2 + 1)^2} = 1. \quad \text{(①)}
$$计算弦长:
$$
|AC| = \sqrt{1 + k^2} \cdot |x_1 – x_2| = \sqrt{1 + k^2} \cdot \sqrt{(x_1 + x_2)^2 – 4x_1x_2}
= \sqrt{1 + k^2} \cdot \sqrt{\left(-\frac{6km}{3k^2 + 1}\right)^2 – 4 \cdot \frac{3m^2 – 12}{3k^2 + 1}}
= \sqrt{1 + k^2} \cdot \sqrt{\frac{36k^2m^2 – 4(3m^2 – 12)(3k^2 + 1)}{(3k^2 + 1)^2}}.
$$计算 $|BD|$:
$$
|BD| = \sqrt{1 + \left(-\frac{1}{k}\right)^2} \cdot |x_B – x_D| = \sqrt{1 + \frac{1}{k^2}} \cdot \left|-\frac{6km}{3k^2 + 1} – 0\right|
= \sqrt{\frac{k^2 + 1}{k^2}} \cdot \frac{6|k||m|}{3k^2 + 1}
= \frac{\sqrt{k^2 + 1}}{|k|} \cdot \frac{6|k||m|}{3k^2 + 1}
= \frac{6|m|\sqrt{k^2 + 1}}{3k^2 + 1}.
$$假设正方形 $ABCD$ 存在,则 $|AC| = |BD|$,
因此
$$
\sqrt{1 + k^2} \cdot \sqrt{\frac{36k^2m^2 – 4(3m^2 – 12)(3k^2 + 1)}{(3k^2 + 1)^2}} = \frac{6|m|\sqrt{k^2 + 1}}{3k^2 + 1}.
$$两边平方并整理得:
$$
\frac{36k^2m^2 – 4(3m^2 – 12)(3k^2 + 1)}{(3k^2 + 1)^2} = \frac{36m^2}{(3k^2 + 1)^2},
$$
即
$$
36k^2m^2 – 4(3m^2 – 12)(3k^2 + 1) = 36m^2.
$$展开并整理:
$$
36k^2m^2 – 12m^2(3k^2 + 1) + 48(3k^2 + 1) = 36m^2,
$$
$$
36k^2m^2 – 36k^2m^2 – 12m^2 + 144k^2 + 48 = 36m^2,
$$
$$
-12m^2 + 144k^2 + 48 = 36m^2,
$$
$$
144k^2 + 48 = 48m^2,
$$
$$
3k^2 + 1 = m^2. \quad \text{(②)}
$$将①代入②得:
$$
\frac{(3k^2 + 4)(3k^2 + 1)}{(3k^2 + 1)^2} = 1,
$$
即
$$
\frac{3k^2 + 4}{3k^2 + 1} = 1,
$$
$$
3k^2 + 4 = 3k^2 + 1,
$$
$$
4 = 1.
$$
该方程无解,不符合题意。综上,存在符合题意的正方形 $ABCD$,其边长为 $\sqrt{6}$ 或 $3\sqrt{2}$。
另外一种思路(我的考场思路)是在韦达定理的基础上,直接根据正方形的条件,用 $A(x_1,y_1),C(x_2,y_2)$ 表示出 $B, D$ 的坐标,然后以 $B$ 在椭圆上、$D$ 在 $y$ 轴上为条件来继续解题。因为这时 $B,D$ 的坐标在代入韦达定理结论后会“非常丑”,所以这种方法的求解难度相比上面的方法更大。
但是经过我和同学们的讨论,我们发现这种方法已经包含了“点代入”法的思想——确定一个点的坐标并用它表示出其他点的坐标。所以如果我们抛弃韦达定理直接走“点代入”呢?
那么你会得到这道题很巧妙且最好算的解法!
方法2:点坐标代入法
思路在上面,直接开始写过程。
先设 $A,C$ 坐标,解出 $B,D$ 坐标。这里怎么解并不太重要。
设 $A(x_1,y_1),C(x_2,y_2)$。不妨设 $ABCD$ 顺时针排列。
由题意,$ABCD$是正方形,则
$$
(x_B-x_D)(x_2-x_1)+(y_B-y_D)(y_2-y_1)=0
$$
$$
(x_B-x_D)^2+(y_B-y_D)^2=(x_2-x_1)^2+(y_2-y_1)^2
$$
得
$$
x_B-x_D=y_2-y_1,y_B-y_D=x_1-x_2
$$
解得
$$
B(\frac{x_1-y_1+x_2+y_2}{2},\frac{x_1+y_1-x_2+y_2}{2})
$$
$$
D(\frac{x_1+y_1+x_2-y_2}{2},\frac{-x_1+y_1+x_2+y_2}{2})
$$
由D在y轴上,知 $x_1+y_1+x_2-y_2=0$,即$x_1+x_2=y_2-y_1$。
那么这样一个“神奇”的条件怎么使用呢?因为椭圆方程中有 $x^2$ 和 $y^2$,所以考虑同时把 $A,C$ 代入椭圆方程并移项,得到平方差,然后便可以利用这个条件进一步用纵坐标表示 $x_1-x_2$,从而得到横纵坐标之间的关系。
因为这种方法涉及到等式两侧同时除 $x_1+x_2$,所以在此之前,我们需要单独讨论 $x_1+x_2=0$ 的情况。这种情况其实正对应着方法1中 $k_{AC}=0$ 的情况。
若 $x_1+x_2=0$,则 $y_2-y_1=0$。
代入 $B,D$坐标,得 $B(0,x_1+y_1),D(0,-x_1+y_1)$。由B在椭圆上,知 $(x_1+y_1)^2=4$,$x_1+y_1=\pm 2$。
与 $\frac{x_1^2}{12}+\frac{y_1^2}{4}=1$ 联立,解得 $x_1=-3,3,0$。
经检验,舍去 $x_1=0$ 的解,则 $|AC|=|2x_1|=6$ ,$|AB|=\frac{6}{\sqrt 2}=3\sqrt 2$
求解横纵坐标关系:(这里是用纵坐标表示横坐标,当然你也可以用横坐标表示纵坐标)
若 $x_1+x_2\neq 0$,则 $y_2-y_1 \neq 0$。
由
$$
\frac{x_1^2}{12}+\frac{y_1^2}{4}=\frac{x_2^2}{12}+\frac{y_2^2}{4}=1
$$
知
$$
x_1^2-x_2^2=-3(y_1^2-y_2^2)
$$
等式两侧同时除以 $x_1+x_2$、$y_2-y_1$,得
$$
x_1-x_2=3(y_1+y_2)
$$
解得
$$
x_1=y_1+2y_2, x_2=-2y_1-y_2
$$
代入 $B$ 点坐标,得 $B(y_2-y_1,2y_1+2y_2)$。
这时我们的未知量只有 $y_1,y_2$ 了,可以开始使用 $B$ 在椭圆上这个条件,得到关于这两个未知量的方程组。
由 $A$ 点在椭圆上,知
$$
\frac{x_1^2}{12}+\frac{y_1^2}{4}=1
$$
代入 $x_1=y_1+2y_2$ 得
$$
y_1^2+y_1y_2+y_2^2=3 \quad \text{(①)}
$$
由 $B$ 点在椭圆上,知
$$
\frac{(y_2-y_1)^2}{12}+\frac{(2y_1+2y_2)^2}{4}=1
$$
展开得
$$
13y_1^2+22y_1y_2+13y_2^2=12 \quad \text{(②)}
$$
②-13①得 $y_1y_2=-3$。代入①得 $(y_1+y_2)^2=0$,$y_1+y_2=0$
发现这种情况其实正对应着方法1中 $k_{AC}$ 不存在的情况。
解得 $y_1,y_2$ 中一个是 $\sqrt 3$,另一个是 $-\sqrt 3 $,$x_1=x_2=\sqrt 3$。
所以 $|AC|=2\sqrt 3$,$|AB|=\frac{2\sqrt 3}{\sqrt 2}=\sqrt 6$
综上,存在符合题意的正方形 $ABCD$,其边长为 $\sqrt{6}$ 或 $3\sqrt{2}$。
方法3:几何转化
其实方法2中的结论 $x_1+x_2=y_2-y_1$ 可以从 $A,C$ 往 $y$ 轴做垂线,通过初中平面几何中倾斜放置正方形的“弦图”看出,并且还可以进一步根据“弦图”得到 $B$ 点坐标。当然我建议使用这种方法找到思路的同学写一个方法2的卷面过程,就不给大家展开了。
方法1完整过程来自参考答案
方法2完整过程来自@abcxyz
方法3来自我自己()
更新时间:2026年1月25日